ASINTOTAS DE FUNCIONES

La asíntota de una función es una recta a la que se aproxima continuamente la gráfica de tal función;​ es decir que la distancia entre las dos tiende a ser cero, a medida que se extienden indefinidamente.

De este concepto aparecen tres subconceptos que se verán a continuación:

 

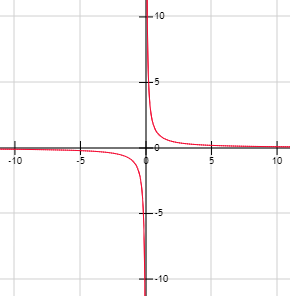
Asíntota Horizontal: Las asíntotas horizontales se distinguen porque cuando la x se hace infinitamente grande, dando un efecto en el grafico como si esta fuese pegada al eje X o Y pero si se observa bien la linea va separada del eje.

 Según consideremos si el limite es +∞ o -∞ se podrá decir si la asíntota horizontal se presenta por la izquierda o por la derecha.

 

 Asíntota Vertical: Para localizar una "asíntota vertical" de una función f (x) basta localizar puntos "k" en donde la función no esté definida. De este modo el límite será infinito y la recta " x=k " será asíntota vertical.

 

Asíntota Oblicua: Si el grado del numerador es mayor que el grado del denominador. Pueden encontrarse en una función hasta dos asíntotas oblicuas distintas. Si el resultado de n es un número real, entonces la recta Y =mx +n será una asíntota oblicua para f (x) por el lado derecho.